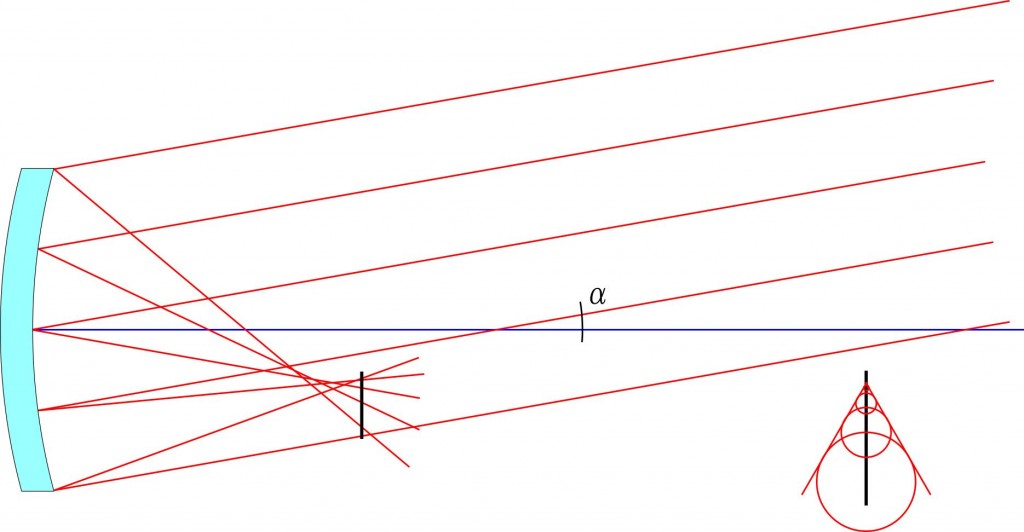
Od strony optycznej, niewątpliwą wadą teleskopów Newtona jest aberracja optyczna zwana komą. Jest to wada pozaosiowa, występująca jedynie w przypadku nieosiowego padania światła na lustra wklęsłe i dotyczy wyłącznie obrazu pozaosiowego. Podczas tworzenia obrazu w teleskopie zwierciadlanym, równoległe promienie światła natrafiają na przeciwległe brzegi lustra o określonej krzywiźnie. O ile w przypadku wiązki światła równoległej do osi optycznej (zwierciadła) krzywizny po przeciwnych stronach osi optycznej zawsze są identyczne, to dla promieni pozaosiowych krzywizna „widziana” przez każdy promień ulega zmianie. Różne krzywizny w przekroju wiązki oznaczają różne ogniskowe dla różnych partii wiązki. Z tego powodu, często określa się komę jako wada zmienności powiększenia w funkcji apertury. Dla żadnej z wiązek pozaosiowych, nie istnieje więc jeden konkretny punkt ogniskowania, co uwidacznia poniższy rysunek:
Rys. 1: Geometryczne odwzorowanie aberracji komatycznej.
Natężenie aberracji komatycznej rośnie proporcjonalnie do odległości obrazu od osi optycznej. Wielkość komy silnie zależy też od światłosiły: W przypadku kątowego pola widzenia koma przyrasta do kwadratu światłosiły, z kolei w przypadku pola liniowego – aż do jej sześcianu!

 Rys. 2: Symulacja widoku Plejad w Newtonie F/4 ze skorygowaną komą i w teleskopie nieskorygowanym.
Rys. 2: Symulacja widoku Plejad w Newtonie F/4 ze skorygowaną komą i w teleskopie nieskorygowanym.
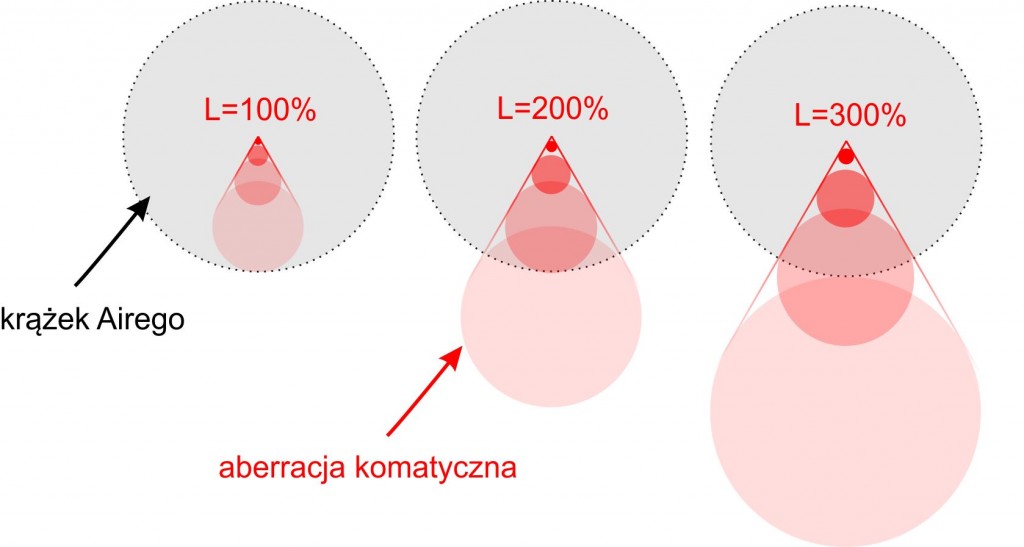
Aby opisać i zrozumieć widoczność komy w teleskopie musimy wprowadzić do uporządkowanego świata geometrii zjawiska dyfrakcji. Otóż dyfrakcja występująca w teleskopach ogranicza minimalny kątowy rozmiar aberracji komatycznej, jaki może zostać odwzorowany w teleskopie do rozmiaru większego niż krążek Airego (rys. poniżej).
Rys. 3: Geometryczna symulacja komy zwierciadła parabolicznego.
Gdy okular teleskopu odwzorowuje krażek Airego o polu widzenia 1 minuty kątowej, nie oznacza to, że koma większa od tej wartości automatycznie zostanie zaobserwowana. Ludzkie oko potrzebuje dużo więcej, niż tylko graniczną 1 minutę kątową, aby dostrzec kształt komy. W praktyce, aby koma mogła zostać dostrzeżona w okularze, powinna mieć długość powyżej 3 minut kątowych, choć dostrzegalność komy w realnych warunkach zależy od wielu czynników, np. od seeingu, kolimacji i jakości okularu. Istnieje jednak uproszczenie, pomocne do obliczania pole widzenia wizualnie wolnego od komy w teleskopie Newtona:
D [mm] = 0,066 x (F)^3.
gdzie D – liniowe pole widzenia, F – światłosiła zwierciadła
Okazuje się, że w teleskopie o światłosile F/6 pole widzenia wizualnie wolne od komy wynosi 14,2 mm, natomiast w teleskopie F/4,7 już tylko 6,85 mm.
Dla obserwatora wizualnego ważniejsza jednak jest nie liniowa, lecz kątowa wielkość obrazu wizualnie wolna od komy. Z racji liniowego wzrostu komy w funkcji odległości od osi optycznej, kątowy rozmiar obrazu wolnego od tej wady nie powinien zmieniać się w funkcji zmian powiększenia w teleskopie o danej światłosile. Co więcej, aberracje własne na brzegu pola widzenia większości okularów astronomicznych są z reguły sporo większe, niż 3 minuty kątowe, dzięki czemu kryterium można „poluźnić” do 6”. Dzięki temu oraz po kilku przekształceniach trygonometrycznych, uzyskujemy kolejną prostą zależność pola widzenia wolnego od komy: D [stopnie] = F^2. Można przedstawić to w formie czytelnej tabeli:
|
Światłosiła reflektora Newtona |
Pole widzenia wolne od komy |
Okulary oferujące pole wizualnie wolne od komy |
|
F/4 |
16° |
– |
|
F/5 |
25° |
– |
|
F/6 |
36° |
Okulary ortoskopowe |
|
F/7 |
49° |
GSO Plossl, TV Plossl |
|
F/8 |
64° |
BP Hyperion, Vixen LVW, SW SWA-58, TV DeLite |
|
F/9 |
81° |
TV Nagler, WO UWAN, Baader Morpheus, ES 82° |
|
F/10 |
100° |
TV Ethos, WO XWA, ES 100° |
Tab. 1: Zależność kątowego rozmiaru obrazu wizualnie wolnego od komy od światłosiły teleskopu.